Direct Gear Design for Spur and Helical Involute Gears

Alexander L. Kapelevich and Roderick E. Kleiss

Dr. Alexander L. Kapelevich is an owner of the consulting firm AKGears of Shoreview, MN, and principal engineer for Kleiss Gears Inc. of Centerville, MN. He has more than 20 years of experience in development of aviation and commercial gear transmissions in Russia and the United States. Roderick E. Kleiss, professional engineer, is owner and president of Kleiss Gears Inc. His company engineers and manufactures high precision, plastic molded gears using the direct gear design approach.

This paper presents an alternative method of analysis and design of spur and helical involute gears.

Introduction

Modern gear design is generally based on standard tools. This makes gear design quite simple (almost like selecting fasteners), economical, and available for everyone, reducing tooling expenses and inventory. At the same time, it is well known that universal standard tools provide gears with less than optimum performance and - in some cases - do not allow for finding acceptable gear solutions. Application specifics, including low noise and vibration, high density of power transmission (lighter weight, smaller size) and others, require gears with nonstandard parameters. That’s why, for example, aviation gear transmissions use tool profiles with custom proportions, such as pressure angle, addendum, and whole depth. The following considerations make application of nonstandard gears suitable and cost-efficient:

• CNC cutting machines and CMM gear inspection equipment make production of nonstandard gears as easy as production of standard ones.
• Cost of the custom cutting tool is not much higher than that of the cutting tool for standard gears and can be amortized if production quantity is large enough.
• The custom gear performance advantage makes a product more competitive and justifies larger tooling inventory, especially in mass production.
• Gear grinding is adaptable to custom tooth shapes.
• Metal and plastic gear molding cost largely does not depend on tooth shape.

This article presents the direct gear design method, which separates gear geometry definition from tool selection, to achieve the best possible performance for a particular product and application.

The direct design approach that is commonly used for most parts of mechanisms and machines (for example, cams, linkages, compressor or turbine blades, etc.) determines their profiles according to the operating conditions and desired performance. Ancient engineers used the same approach for gear design, developing the tooth shape first and then figuring out a way to get it. During the technological revolution in the 19th century, the highly productive gear generating process was developed. New machine tools required complicated and expensive tools, hobs or gear shapers. Common parameters of the cutting tool (generating rack) were standardized. This has made modern involute gear design indirect because the gear tooth profiles depend on a preselected, usually standard set for parameters of the generating rack (diametral pitch or module, pressure angle, addendum and dedendum proportions, tip radii, etc.) and its location (addendum modification or x-shift), relative to a standard pitch diameter of the gear.

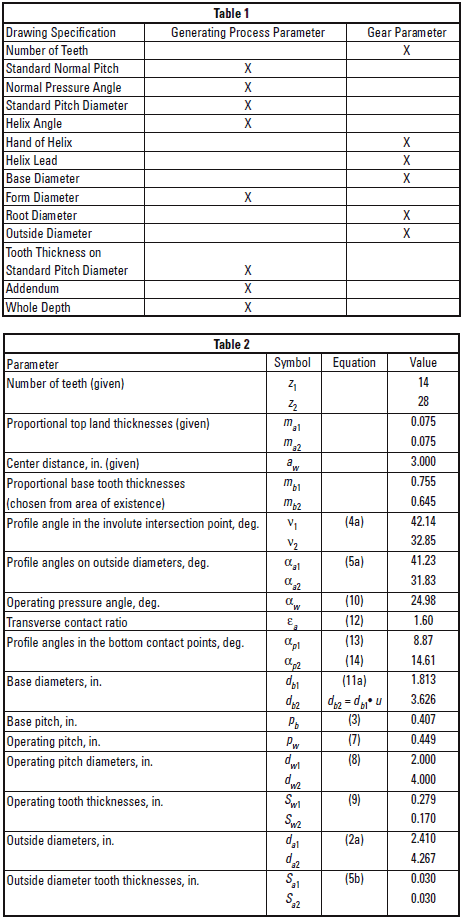
Table 1 shows a typical helical gear specification, where gear parameters and the generating process (rack and its location) parameters are separated. The gear as a part does not have a pressure angle, pitch diameter, diametral pitch or module, helix angle, addendum or addendum modification. All these parameters are related to the tool and generating process. The involute gear has a number of teeth, base diameter, outside diameter, helical lead, and base tooth thickness.

The generating rack method of gear design does not guarantee sufficient gear design. The minimum number of pinion teeth is limited to avoid undercut. The addendum modification or xshift of the generating rack is introduced to balance bending fatigue stresses and specific sliding for pinion and gear, and to reduce undercut for pinions with small numbers of teeth.

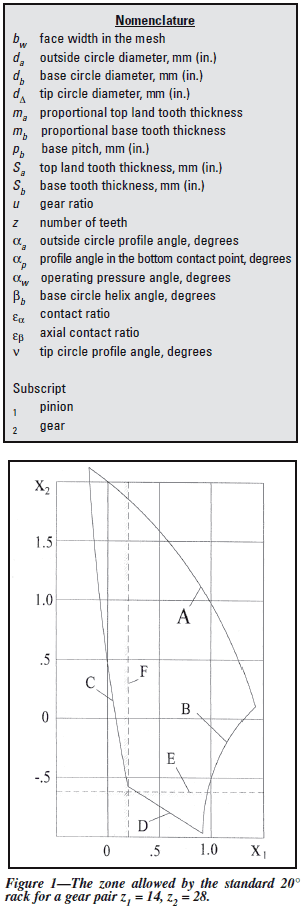
Why must tooth profiles be modified or corrected at the very earliest stages of the gear design? The modification must occur so early because the traditional approach is limited by its own arbitrary selection of generating rack parameters. The zone depicted (Ref. 1) in x-shift coefficient coordinates x₁ and x₂, for a pair of spur gears z₁ = 14, z₂ = 28 formed by a standard generating rack with 20° pressure angle is shown in Figure 1. The zone shown contains all gear combinations that can be produced using this particular generating rack. Its area is limited by the minimum contact ratio for spur gears ε_α = 1.0 (isogram A), the sharp tip of the pinion (isogram B), and the tip-fillet interference (isograms C and D). The undercut isograms E and F put additional limitations on the zone area. Other available gear combinations exist outside the zone borders, but in order to realize them, the generating rack parameters would have to be changed. In other words, a range of possible gear combinations is limited by the cutting tool (generating rack) parameters and the machine tool setup (x-shift).

Direct gear design is the way to obtain all possible gear combinations by analyzing their properties without using any of the generating process parameters. Those parameters can be defined after the gear design is completely finished.

There were attempts to use the base circle as a foundation for the involute gear theory, separating the gear analysis from the gear generating process. Professor E.B. Vulgakov developed the so-called theory of generalized parameters for involute gears (Ref. 2). J.R. Colbourne (Ref. 3) described an alternative definition of the involute without using the generating rack. The self-generating method "gear forms gear" was proposed for plastic molded gears (Refs. 4 and 5). According to this method, the top land of the tooth of one of the gears forms the fillet of the mating gear and vice versa. At a glance, it looks similar to a gear shaping or gear rolling process, but the fact that both gears are described without the generating rack parameters makes a difference in their geometry and characteristics.

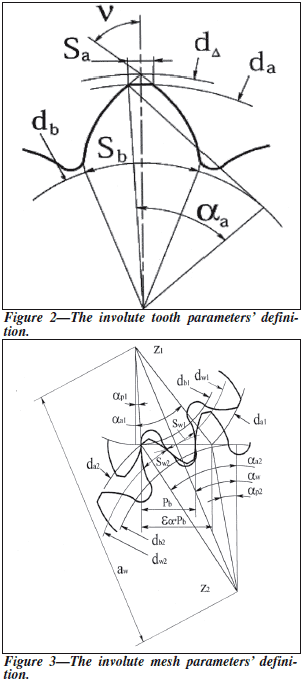
Involute Tooth Parameters

An involute tooth is formed by two involutes unwound from the base circle d_b, outside circle diameter d_a and fillet (Ref. 2) (see Fig. 2). Unless otherwise stated, the following equations are correct for spur gears and for helical gears in the transverse section (the section perpendicular to the axis of the gear). Equation numbers with alphabetic modifiers are given for use in the numeric examples listed in Tables 2, 3 and 4.

The profile angle in the intersection point of the two involutes (tip angle) is

The profile angle on the outside diameter d_a is

The base pitch is

The proportional base tooth thickness is

The proportional top land thickness is

Involute Gear Mesh Parameters

Figure 3 shows the zone of tooth action of the pinion and the gear in close mesh (backlash is zero). The close mesh condition is

The operating pressure angle can be found by substitution of Equation 6 with 7, 8, and 9:

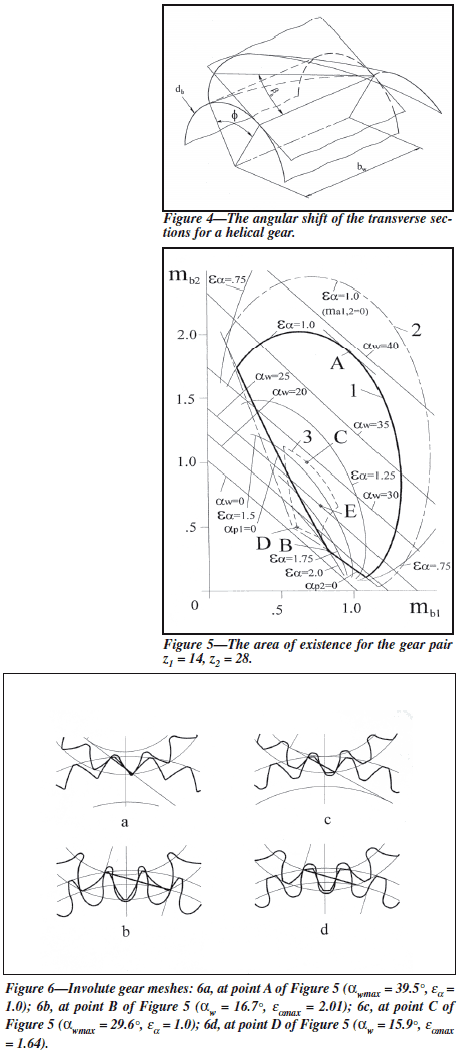
The operating pressure angle is a gear mesh parameter and it cannot be defined for one separate gear.

The center distance is

The contact ratio (for spur gears and for helical gears in the transverse section) is

The profile angle in the bottom contact point must be larger than or equal to zero to avoid involute undercut:
for the pinion

The axial contact ratio for helical gears is

The fillet profile must provide a gear mesh with sufficient radial clearance to avoid tip-fillet interference. The fillet also must provide necessary tooth bending fatigue resistance and mesh stiffness. The direct gear design approach allows selection of any fillet profile (parabola, ellipsis, cubic spline, etc.) that would best satisfy those conditions. This profile is not necessarily the trochoid formed by the rack or shaper generating process.

Tool geometry definition is the next step in direct gear design. This will depend on the actual manufacturing method. For plastic and metal gear molding, gear extrusion, and powder metal gear processing, the entire gear geometry - including correction for shrinkage - will be directly applied to the tool cavity. For cutting tools (hobs, shaper cutters), the reverse generating approach "gear forms tool" can be applied. In this case, the tooling pitch and profile (pressure) angle are selected to provide the best cutting conditions.

Area of Existence of Involute Gears

Figure 5 shows an area of existence for a pinion and gear with certain numbers of teeth z₁, z₂, and proportional top land thicknesses m_a1, m_a2 (Ref. 2). Unlike the zone shown in Figure 1, the area of existence in Figure 5 contains all possible gear combinations and is not limited to restrictions imposed by a generating rack. This area can be shown in proportional base tooth thicknesses m_b1– m_b2 coordinates or other parameters describing the angular distance between two involute flanks of the pinion and gear teeth, like α_a1– α_a2 or ν₁– ν₂. A sample of the area of existence for a pair of gears z₁ = 14, z₂ = 28, m_a1 = m_a2 = 0.075 is shown in Figure 5. The area of existence includes a number of isograms reflecting constant values of different gear parameters, such as operating pressure angles α_w, contact ratios ε_α, etc. The area of existence of spur gears (thick line 1) is limited by isogram ε_α = 1.0, and undercut isograms α_p1 = 0°, α_p2 = 0°. Helical gears can have a transverse contact ratio less than 1.0 because the axial contact ratio can provide proper mesh. The area of existence of helical gears is therefore much greater. Each point on the area of existence reflects a pair of gears with dimensionless properties that can fit a particular application. These properties are pressure angles, contact ratios, pitting resistance geometry factor I, specific sliding ratio, etc.

The absolute area of existence includes spur gear combinations with any values of proportional top land thicknesses between m_a1 = m_a2 = 0 to m_a1 = m_b1 and m_a2 = m_b2 (phantom line 2). This area is substantially larger than the area with given values of proportional top land thicknesses. The zone for a standard generating rack with 20° pressure angle (as shown in Fig. 1) is only a fractional part of the available area of existence as shown by hidden line 3 in Figure 5. An application of a traditional gear generating approach for gear pairs outside the zone outlined by hidden line 3 requires selection of a generating rack with different parameters. The generation of some gear combinations (top left and bottom right corners of the area of existence shown in Fig. 5) will require different generating racks for the pinion and for the gear.

Analysis of the area of existence shows how many gear solutions could be left out of consideration if a traditional approach based on a predetermined set of rack dimensions is applied. For example, spur gears with a high operating pressure angle (point A on the Figure 5, where the operating pressure angle α_w = 39.5°, contact ratio ε_α = 1.0), or with a high contact ratio (point B on the Figure 5, where contact ratio ε_α = 2.01, operating pressure angle α_w = 16.7°) could not be produced with standard rack dimensions. Figures 6a and 6b show these gears. Figures 6c and 6d are the gears that are achievable using a standard generating rack that are presented by points C (α_w = 29.6°, ε_α = 1.0) and D (α_w = 15.9°, ε_α = 1.64) in Figure 5. Even gears with the same operating pressure angle (point E in Fig. 5) look quite different (Fig. 7). The standard designed gear pair (Fig. 7b) has almost sharp-pointed pinion teeth and short and stubby gear teeth with excessive top land tooth thickness. The direct designed gear pair shown in Figure 7a has a contact ratio ε_α = 1.47. The standard designed gear pair has a contact ratio of only ε_α = 1.16 in close mesh. In an actual application with real manufacturing tolerances and operating conditions, the contact ratio of a standard designed gear pair could be reduced to an unacceptable level ε_α < 1.0.

Synthesis of Gearing: Numerical Examples

There are several ways to define gear parameters using the direct gear design approach. This article considers some of them.

Area of existence is known. The initial data for the synthesis of a pair of gears (z₁, z₂, m_a1, m_a2) could be taken from the area of existence at some particular point. The coordinates of this point and center distance a_w describe all operating gear parameters. This calculation procedure and numerical example are presented in the Table 2.

Area of existence is not known. Typical problems could be finding the maximum pressure angle if the transverse contact ratio is chosen or finding the maximum transverse contact ratio if the pressure angle is chosen. Both of these cases require finding the point of area of existence where isograms a_w and ε_α have the same tangent. This condition is described (Ref. 2) as:

The fillet between teeth is not involved in gear mesh operation, but its shape greatly affects gear performance and durability. In traditional gear design, the fillet profile is a function of the cutter shape and the machine tool setup. It typically has excessive radial clearance resulting in high bending stresses. Direct gear design does not limit fillet shape definition. One possibility is to describe the fillet profile as a trace of the top part of the mating gear tooth (with corresponding minimum radial clearance) (Refs. 4 and 5). Application of finite element analysis allows for forming the fillet profiles to balance and minimize bending stresses.

Extreme Parameters of Involute Gears

Point A (tangent point of isograms ε_α = 1.0 and α_w = max) of the area of existence describes gears with the maximum achievable operating pressure angle. There is no such limit for helical gears because a lack of the transverse contact ratio (ε_α < 1.0) is compensated by the axial contact ratio ε_β. A sample of a helical gear with high operating pressure angle (Ref. 6) is shown in Figure 8. In Figure 5, the point B (intersection point of interference isograms α_p1 = 0° and α_p2 = 0°) of the area of existence describes the gears with the maximum achievable transverse contact ratio. Table 5 presents maximum values for operating pressure angle α_w^A (Point A of the area of existence) and transverse contact ratio ε_α^B (Point B of the area of existence) for gear pairs with different numbers of teeth and the proportional top land thicknesses m_a1 = m_a2 = 0.075. An example of a spur gear mesh with a high contact ratio is shown in Figure 9.

Spur gears (contact ratio ε_α ≥ 1.0) with a minimum possible number of teeth (Ref. 2) are shown in Figure 10. The minimum possible number of teeth for helical gears is not limited by transverse contact ratio and could be as few as one (Ref. 6). An example of a helical gear with the number of teeth z₁ = z₂ = 1 is shown in Figure 11.

Involute Gears with Asymmetric Tooth Profile

Opposite flanks (profiles) of the gear tooth are functionally different for most gears. The workload on one profile is significantly higher and/or is applied for longer periods of time than on the opposite one. The asymmetric tooth shape accommodates this functional difference.

The design intent of asymmetric teeth is to improve performance of main contacting profiles by degrading opposite profiles. These opposite profiles are unloaded or lightly loaded, and usually work for a relatively short period. The improved performance could mean increasing load capacity or reducing weight, noise, vibration, etc.

Degree of asymmetry and drive profile selection for these gears depends on the application. Asymmetric profiles make it possible to manage tooth stiffness and load sharing while keeping a desirable pressure angle and contact ratio on the drive profiles.

Direct design of gears with asymmetric teeth is considered in detail in other articles (Refs. 7 and 8), covering topics such as analysis and synthesis of asymmetric gearing, area of existence, and applications. Examples of gears with asymmetric tooth profiles are shown in Figure 12. Gears with asymmetric teeth should be considered for gear systems that require extreme performance, like aerospace drives. They are also applicable for mass production transmissions where the share of the tooling cost per one gear is relatively insignificant. The most promising application for asymmetric profiles is with molded gears and powder metal gears. Molded gear tooling usually requires a custom shape, so the asymmetric profile does not significantly affect cost.

Summary

Direct gear design is an alternative approach to traditional gear design. It allows analysis of a wide range of parameters for all possible gear combinations in order to find the most suitable solution for a particular application. This optimum gear solution can exceed the limits of traditional rack generating methods of gear design.

Direct gear design for asymmetric tooth profiles opens additional reserves for improvement of gear drives with unidirectional load cycles that are typical for many mechanical transmissions.

Acknowledgments
The authors express deep gratitude to Gear Technology technical editors Robert Errichello of Geartech, located in Townsend, MT, and Dan Thurman for their help in preparing this article.

References
1.  Groman, M.B. "The Zones of Involute Mesh," Vestnik Mashinostroeniya, 1962, Issue 12, pp. 12-17 (in Russian).
2.  Vulgakov, E.B. Theory of Involute Gears, Mashinostroenie, Moscow, 1995 (in Russian).
3. Colbourne, J.R. The Geometry of Involute Gears, Springer-Verlag, New York, 1987.
4.  ANSI/AGMA 1006-A97, "Tooth Proportions for Plastic Gears," Appendix F "Generating Gear Geometry Without Racks," AGMA, Alexandria, VA, 1997.
5.  Kleiss, R.E., A.L. Kapelevich, and N.J. Kleiss. New Opportunities with Molded Gears, AGMA Fall Technical Meeting, Detroit, October 3-5, 2001, (01FTM9)
6.  Vulgakov, E.B. and A.L. Kapelevicich. "Expanding the range of involute helical gearing," Vestnik Mashinostroeniya, 1982, Issue 3, pp. 12-14 (in Russian). Translated to English, Soviet Engineering Research, Vol. 2, Issue 3, 1982, pp. 8-9.
7.  Kapelevich, A.L. "Geometry and design of involute spur gears with asymmetric teeth," Mechanism and Machine Theory, 2000, Issue 35, pp. 117-130.
8.  Litvin, F.L., Q. Lian, and A.L. Kapelevich. "Asymmetric modified gear drives: reduction of noise, localization of contact, simulation of meshing and stress analysis," Computer Methods in Applied Mechanics and Engineering, 2000, Issue 188, pp. 363-390.